📌 목차
왜 수학적 모델링이 법·사회 탐구에 유리할까?
법과 사회 영역은 통상적으로 인문·사회학적 접근이 많지만, 수학적 모델링을 접목하면 훨씬 더 논리적이고 과학적인 분석이 가능합니다.
예를 들어 범죄 발생, 교통 혼잡, 세금 정책, 감염병 확산 등은 모두 통계·함수·시뮬레이션 등 수학적 도구로 설명할 수 있는 사회 현상입니다.
📌 생기부에서 주는 강점
- 융합형 탐구: 사회 이슈 + 수학 논리 = 통합 사고력 어필
- 진로 연계: 법학, 사회학, 정책학, 행정, 경찰, 경제 등
- 탐구 심화도 ↑: 단순 이론 나열이 아닌 실제 문제 해결로 연결
수학을 사회에 적용한 탐구는 진로 희망 학과에도 강력한 설득력을 줍니다.


주제 ① 범죄 발생 예측 모델링
도시 내 범죄 발생 패턴을 수학적으로 분석해보는 탐구입니다.
공공 데이터를 기반으로 회귀분석 또는 시계열 분석을 활용할 수 있습니다.
✅ 활용법:
- 서울 열린데이터광장 등에서 지역별 범죄 발생 통계 수집
- 시간·요일·장소 별 발생 빈도 분석 → 위험 구역 예측
- 결과를 토대로 예방 정책 제안 또는 CCTV 우선 설치 지역 제시
✅ 생기부 표현 포인트: “범죄 발생률을 회귀모델로 분석하고, 수학적 예측을 기반으로 사회 안전망 강화 방향을 탐색함.”
주제 ② 전염병 확산 방역 정책 모델링
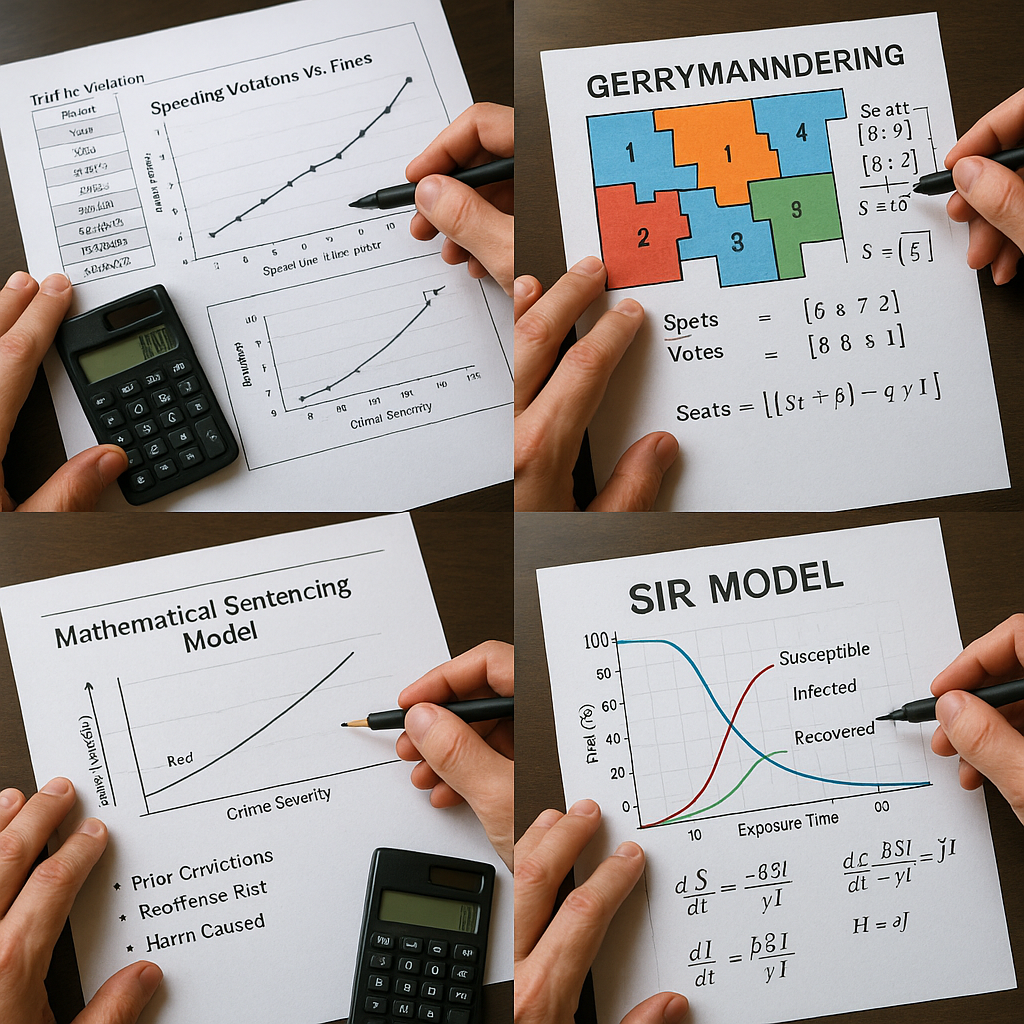
SIR 모델을 활용하여 감염병 확산과 방역 효과를 시뮬레이션하는 탐구입니다.
✅ 활용법:
- SIR (감수성-감염-회복) 모델 또는 SEIR 모델 수식 활용
- 사회적 거리두기 시뮬레이션 → 확산 곡선 변화 확인
- 백신 접종률 변화에 따른 결과 시각화
✅ 생기부 표현 포인트: “SIR 모델을 활용해 감염병 확산 양상을 수학적으로 예측하고, 방역 정책의 효과성을 수치로 비교 분석함.”
주제 ③ 대중교통 최적화 모델링

교통 문제 해결을 수학적 그래프 이론으로 탐구하는 주제입니다.
최단경로 알고리즘이나 네트워크 분석 기법을 활용할 수 있습니다.
✅ 활용법:
- 도시 대중교통 노선 데이터를 간선·정점으로 구성한 그래프화
- 최단 경로, 교통량 예측, 병목 구간 탐색
- 도보 + 대중교통 조합 모델로 이동 효율 개선 제안
✅ 생기부 표현 포인트: “교통망 데이터를 그래프 이론으로 구조화하고, 최적 경로 알고리즘을 통해 이동 효율성을 수학적으로 분석함.”
주제 ④ 소득 불평등과 조세 모델링
지니계수, 로렌츠 곡선 등 수학적 불평등 지표를 활용한 경제·사회 정책 탐구입니다.
✅ 활용법:
- 소득 분포 데이터를 기반으로 지니계수 계산
- 누진세 모델을 수학 함수로 표현 → 세금 효과 시뮬레이션
- 조세 정책별 소득 재분배 효과 비교
✅ 생기부 표현 포인트: “수학적 지표(지니계수, 로렌츠 곡선)를 활용해 소득 불평등을 분석하고, 누진세 정책의 형평성 효과를 수치 기반으로 탐색함.”